4.1: Teaching for Problem-Solving
This approach to problem-solving in the mathematics classroom was proposed and published by Stanford Professor of Mathematics George Polya in 1945. At a time when mathematics was primarily being taught by means of drills and examples, and a new emphasis for specialized science and math curriculum was being interpreted by war, this old idea emerged and re-emphasized insight, creative-thinking, and a holistic approach to understanding and teaching mathematics.
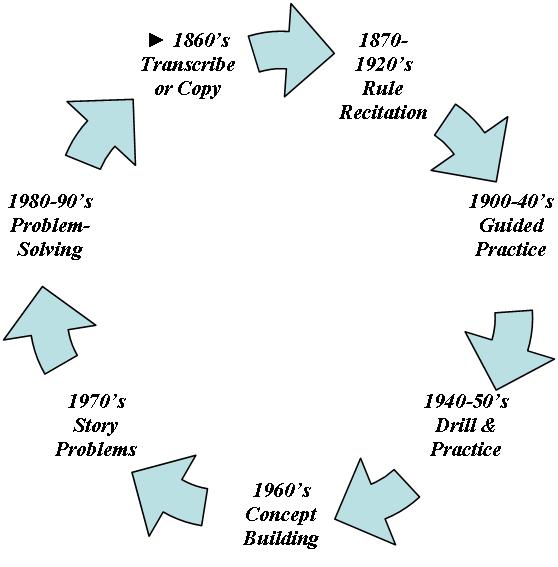
From the inception of formal education in the United States, mathematics has slowly taken root in the overall curriculum. Its importance in education has paralleled its importance to American Society; as times changed, so did mathematics instruction. Some instructional styles have come and gone, only to return again as a modern approach. Although problem-solving has stylistically experienced waves of importance, it was not recognized as a standard until the 1980’s, when the National Council of Teachers of Mathematics proclaimed, “The Decade of Problem-Solving.” Polya’s approach to the issue was regarded as the most appropriate, and although other ideas were being introduced, many of the approaches could still be broken down to fit Polya’s framework.
While today’s good math instruction is considered a balance of the above styles and trends, we recognize that, while many disciplines contribute the necessary tools, nowhere else in the curriculum are students formally exercising creative thought processes and using inductive and deductive reasoning. Problem-solving is at home in the mathematics classroom. So, how do we define this objective?
Problem-solving may have been best defined by the psychologist John Hayes, author of The Complete Problem-Solver. He defined the process of problem solving like bridging the gap. In other words, if you do not know the method to get from where you are to where you want to be, you are faced with a problem to be solved. From this definition, I think it is important to acknowledge that gap. To a student, the gap is a void—unexplored space, unfamiliar territory that is both confusing and intimidating. However, as the teacher, this gap is likely not problematic at all. We are familiar with the problem and several methods of solving it. Therefore in presenting this exercise we are not problem-solving with our students, because we are not problem-solving ourselves. With this definition in mind, is it possible to teach problem-solving? Even the mathematicians struggle with this question.
Polya’s fundamental approach outlines the following four steps: 1) understanding the problem, 2) devising a plan, 3) carrying-out the plan, and 4) looking back at the problem. But before these steps are initiated, I believe it is important that teachers ensure students’ motivation by selecting models that are interesting and appropriate in rigor.
Understanding the problem requires the ability to articulate precisely the nature of the starting and ending points. Students may find it necessary to break the problem down into smaller components of known, unknown, and conditional information. It is even appropriate at this level of developing understanding for them to speculate or make a guess as to the solution. The potential value in restating the problem should not be overlooked here either. Introducing a slightly altered vocabulary or verbal structure can prove enlightening and offer a new perspective.
Polya’s other major contribution to problem-solving was the clear application of heuristics. Heuristics are the methods used to make discoveries—a problem-solving toolbox. This is the biggest contribution that other disciplines make to the art of problem-solving and should be recognized as such. In order to devise a plan, step two, students have to ask a lot of questions, sound questions that can lead them, although sometimes gradually, to that light-bulb or Ah-Ha-moment. They should be encouraged to ask, “Have I seen this problem or one like it before?” Here are just a few of the other heuristics that all teachers in all disciplines should value and model for students every day.
Draw a picture or diagram
Define or redefine terms
Consult history and past experiences
Rely upon intuition
Analogize or solve an auxiliary problem for the sake of this one
Check your results
Try the Inventor’s Paradox (attempt a more ambitious problem)
Find practical and/or natural examples
Experiment (trail and error)
Value subconscious work (periods of rest and disconnect)
Consult the wisdom of proverbs
Generalize the problem
Work backwards from a characteristic solution
Use results of failed attempts to solve
When appropriately modeled, these tools are critical observations for students to develop their own problem-solving ability.
While devising a plan requires a lot of concentration, knowledge, trials and frankly luck, the third step of carrying-out the plan is relatively painless. Each step of the plan must be patiently executed and checked. Each step is not only checked for correctness, but for consistency with the plan. With each step students should realize whether they are getting closer to the next step or to the solution.
Finally, the reflective process of looking back at the problem offers valuable perspective. In the case of correctness, this is not the final step, but a circular one that sends students back to steps one and two encouraged by new findings. In the event that a successful solution has been found, it is important to reexamine and reconsider the result. Teachers should pose the following questions to students. How exhaustive is the solution? Can the knowledge be consolidated? How was the overall ability to solve any problem enhanced? Can the arguments and results be checked? Can the result or method be used to solve some other problem?
The following study was performed on students using Polya’s model. In a series of problem-solving exercises, students were timed to find out how much time various students spend in each of the four stages. The students who were identified as “problem-solvers” spent a disproportionate amount of time in stage two, devising the plan. They easily understood the problem, efficiently carried out their plans, reflected objectively. Most interesting to me was that the time spent in stage two was not contiguous. They often bounced back to stage two to try new approaches and revise their thoughts, ideas and plans.
And what separates the “problem-solvers” from the rest of the students? Some would say it is readiness. Jean Piaget’s final stage of cognitive development is known as formal operational thought and is further described in expectation 2.1: Individual Development. In this stage the ability to reason blossoms. The expectation for higher reasoning and thought processes is likely not attainable by adolescents who have not yet reached this final cognitive developmental stage. Courses such as Geometry should be taken perhaps after a second year of Algebra or other math course that requires less abstraction, picking up Geometry when formal thought processes come later. Forcing the issue onto a student who is clearly not ready will create dislike and discouragement.
It is my belief that all students possess the potential to use the full capacity of all their faculties. Perhaps problem-solving cannot be taught in an instructional sense, but as teachers we should consciously model the approach. Nowhere does the ability of a good teacher to model not-knowing (as outlined in expectation 1.2: Teacher as Learner) have a more lasting impact on students than for decision-making and problem-solving. Teachers should ask leading questions of themselves aloud to engage students in the steps of discovery, and they should identify and recognize meaningful, emotional and successful attempts by their students to do the same. Problem-solving is a process of discovery, and teachers need to unobtrusively provide the techniques necessary for students to develop independent work that enriches their own problem-solving ability.
The National Council for Teachers of Mathematics (NCTM) understands the leading role that mathematics plays in the problem-solving curriculum of our nation's high schools. Resources such as publications (e.g. Problem-Solving, and Teaching Mathematics Through Problem-Solving), lessons and activities are available from the council to assist teachers in the classroom. Indiana standards also reflect the importance of using problem-solving throughout all mathematical content curriculum.
My experiences student teaching and substituting gave me the opportunity to apply some of my thoughts about the true meaning of mathematics to the majority of high school students. With the exception of future engineers, our students should study math (in particular geometry) in order to learn how to figure stuff out. In class, I often tried to implement fun, problem-solving activities into the curriculum to relate this fundamental importance. This was particularly fun with Investigative Geometry students, as that curriculum was very loose, and we had the freedom to stray, linger, and toy with some fun, seemingly non-mathematical (to them) activities like map coloring. We also addressed the question of possible solutions (number 7, number 27, number 28, number 29). Problems may have more than one solution, exactly one solution, or no solution at all?
When the naturally inquisitive approach to mathematics using puzzles, logic, games, etc. is introduced to students, their minds become more receptive to the concepts and I enjoy seeing the pride in their eyes when they are able to "figure something out" that the rest of the class may still be wrapping their brains around.
